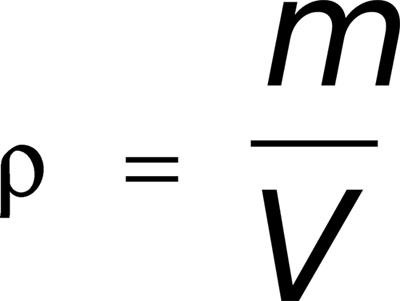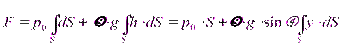- Чем отличается плотность от удельного веса?
- Что есть плотность
- Что есть удельный вес
- Различия между удельным весом/плотностью
- Удельный вес
- Определение удельного веса
- Формула удельного веса
- Разница между весом и массой
- Разница между удельным весом и плотностью
- УВ – что это такое?
- В чем отличия
- Единицы измерения удельного веса
- Металлы с наибольшим и наименьшим удельным весом
- Удельный вес других материалов
- Как рассчитать удельный вес металлов
- Плотность и удельный вес
Чем отличается плотность от удельного веса?
Для ответа на заданный вопрос никак не обойтись без чёткого знания самих определений — с этого и начнём.
Что есть плотность
В первом приближении определение плотности кажется простым и понятным: плотность есть скалярная физическая величина (характеристика вещества), задаваемая как отношение собственной массы тела к общему объёму, этим телом занимаемому. Однако намётанный глаз сразу подметит «скользкое» место, а именно: о каком именно состоянии тела идёт речь, насколько оно однородно? Действительно, газ или жидкость (с некоторыми ограничениями) — тела в бытовом понимании по сути своей изотропные (то есть с характеристиками, одинаковыми в пределах интересующего физического объёма и не зависящими от выбранного направления в этом объёме), однако как быть с твёрдыми телами?
В предельном случае это можно продемонстрировать на твёрдом сыпучем материале, где в одном общем объёме находятся и частички самого материала, и пустоты между ними (хорошо учившие физику в школе попутно возразят, что примерно такую же картину можно получить и с газами/жидкостями, если начать «дробить» их до молекулярного/атомного уровня). Поэтому вышеприведённое определение подразумевает среднюю (иначе — усреднённую) характеристику тела для выбранного характеристического размера, а для сыпучих тел отдельно вводятся понятия «истинной плотности» (усреднённая характеристика, рассчитываемая только по фактическому объёму самих частиц) и «насыпной плотности» (расчётная характеристика для сыпучего материала с учётом всех его пустот — но без дополнительного уплотнения).
Перед переходом ко второму интересующему определению не лишним будет напомнить, что также существует и иногда практически используется на производстве термин «удельная плотность«, задаваемый как отношение плотности интересующего объекта к плотности вещества-эталона (для газов и жидкостей таковыми эталонами типично служат вода и воздух). Для оперирования удельной плотностью важно, чтобы и объект, и эталон находились при одинаковой температуре/давлении (причина в том, что в различных системах измерений эти «стандартные величины» могут браться за условную «точку отсчёта» по-разному).
Что есть удельный вес
Под удельным весом понимается векторная физическая величина, определяемая как отношение веса тела (веса его вещества) к занимаемому телом объёму. Иначе говоря, удельный вес численно равен произведению между ускорением свободного падения и плотностью вещества (на всякий случай напомним, что вес тела — это сила действия тела на опору/подвес либо иное его крепление в гравитационном поле).
Изредка также используется не имеющее отношения к вышеуказанному частное определение, где под удельным весом понимается безразмерное число, указывающее, во сколько раз интересующая субстанция тяжелее воды (в условиях её максимальной плотности, при 4 °C) при равном объёме.
Помимо привычной бытовой неразберихи в виде отождествления массы и веса, применительно к рассматриваемому случаю нужно упомянуть ошибочное отождествление, вытекающее из использования похожей размерности в технической системы единиц МКГСС, где удельный вес задаётся как [килограмм-сила / метр кубический] (кгс/м³).
Различия между удельным весом/плотностью
Из сказанного выше видно, что исключительно мнимая схожесть плотности и удельного веса порождается минимум двумя факторами: общей похожестью построения их определений и типичным ошибочным бытовым отождествлением веса и массы. Плотность и удельный вес — это кардинально различающиеся понятия.
Вот их наиболее важные отличия, которые следует знать (помимо определений):
Источник
Удельный вес
Среди множества параметров, характеризующих свойства материалов существует и такой как удельный вес. Иногда применяют термин плотность, но это не совсем верно. Но так или иначе эти оба термина имеют собственные определения и имеют хождение в математике, физике и множестве других наук, в том числе и материаловедении.
Определение удельного веса
Физическая величина, являющаяся отношением веса материала к занимаемому им объему, называется УВ материала.
Материаловедение ХХI века далеко ушло вперед в и уже освоены технологии, которые каких-то сто лет назад считались фантастикой. Эта наука может предложить современной промышленности сплавы, которые отличаются друг от друга качественными параметрами, но и физико-техническими свойствами.
Для определения того, как некий сплав может быть использован для производства целесообразно определить УВ. Все предметы, изготовленные с равным объемом, но для их производства был использованы разные виды металлов, будут иметь разную массу, она находится в четкой связи с объемом. То есть отношение объема к массе это есть некое постоянное число, характерная для этого сплава.
Для расчета плотности материала применяют специальную формулу, имеющую прямую связь с УВ материала.
Формула удельного веса
Формулу расчета УВ выглядит как отношение веса к объему. Для подсчета УВ допустимо применять алгоритм расчета, который изложен в школьном курсе физики.
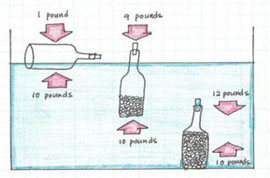
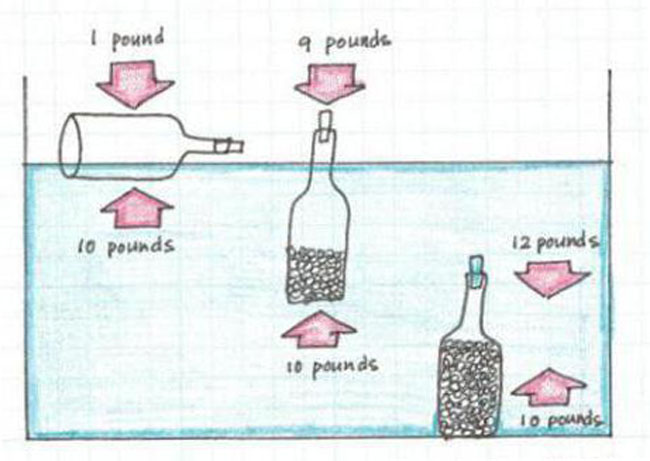
Для этого необходимо использовать закон Архимеда, точнее определение силы, которая является выталкивающей. То есть груз с некоей массой и при этом он держится на воде. Другими словами на него влияют две силы – гравитации и Архимеда.
Формула для расчета архимедовой силы выглядит следующим образом
где g – это УВ жидкости. После подмены формула приобретает следующий вид F=y×V, отсюда получаем формулу УВ груза y=F/V.
Разница между весом и массой
В чем состоит разница между весом и массой. На самом деле в быту, она не играет ни какой роли. В самом деле, на кухне, мы не делаем развития между весом курицы и ее массой, но между тем между этими терминами существуют серьезные различия.
Эта разница хорошо видна при решении задач, связанных с перемещением тел в межзвездном пространстве и ни как имеющим отношения с нашей планете, и в этих условиях эти термины существенно различаются друг от друга.
Можно сказать следующее, термин вес имеет значение только в зоне действия силы тяжести, т.е. если некий объект находиться рядом с планетой, звездой и пр. Весом можно называть силу, с которой тело давит на препятствие между ним и источником притяжения. Эту силу измеряют в ньютонах. В качестве примера можно представить следующую картину — рядом с платным образованием находиться плита, с расположенным на ее поверхности неким предметом. Сила, с которой предмет давит на поверхность плиты и будет весом.
Масса тела напрямую связана с инерцией. Если детально рассматривать это понятие то можно сказать, что масса определяет размер гравитационного поля создаваемого телом. В действительности, это одна из ключевых характеристик мироздания. Ключевое различие между весом и массой заключается в следующем — масса не зависит от расстояния между объектом и источником гравитационной силы.
Для измерения массы применяют множество величин – килограмм, фунт и пр. Существует международная система СИ, в которой применяют привычные, нам килограммы, граммы и пр. Но кроме нее, в многих странах, например, Британских островах, существует собственная система мер и весов, где вес измеряют в фунтах.
Разница между удельным весом и плотностью
УВ – что это такое?
Удельный вес – это есть отношение веса материи к его объему. В международной системе измерений СИ его измеряют как ньютон на кубический метр. Для решения определенных задач в физике УВ определяют следующим образом – насколько обследуемое вещество тяжелее, чем вода при температуре 4 градусов при условии того, что вещество и вода имеют равные объемы.
По большей части такое определение применяют в геологических и биологических исследованиях. Иногда, УВ, рассчитываемый по такой методике, называют относительной плотностью.
В чем отличия
Как уже отмечалось, эти два термина часто путают, но так как, вес напрямую зависим от расстояния между объектом и гравитационным источником, а масса не зависит от этого, поэтому термины УВ и плотность различаются между собой.
Но необходимо принять во внимание то, что при некоторых условиях масса и вес могут совпадать. Измерить УВ в домашних условиях практически невозможно. Но даже на уровне школьной лаборатории такую операцию достаточно легко выполнить. Главное что бы лаборатория была оснащена весами с глубокими чашами.
Предмет необходимо взвесить при нормальных условиях. Полученное значение можно будет обозначить как Х1, после этого чашу с грузом помещают в воду. При этом в соответствии с законом Архимеда груз потеряет часть своего веса. При этом коромысло весов будет перекашиваться. Для достижения равновесия на другую чашу необходимо добавить груз. Его величину можно обозначить как Х2. В результате этих манипуляций будет получен УВ, который будет выражен как соотношение Х1 и Х2. Кроме вещества в твердом состоянии удельных можно измерить и для жидкостей, газов. При этом замеры можно выполнять в разных условиях, например, при повышенной температуре окружающей среды или пониженной температуры. Для получения искомых данных применяют такие приборы как пикнометр или ареометр.
Единицы измерения удельного веса
В мире применяют несколько систем мер и весов, в частности, в системе СИ УВ измеряют в отношении Н (Ньютон) к метру кубическому. В других системах, например, СГС у удельного веса используется такая единица измерения д(дин) к сантиметру кубическому.
Металлы с наибольшим и наименьшим удельным весом
Кроме того, что понятие удельного веса, применяемое в математике и физике, существуют и довольно интересные факты, например, об удельных весах металлов из таблицы Менделеева. если говорить о цветных металлах, то к самым «тяжелым» можно отнести золото и платину.
Эти материалы превышают по удельному весу, такие металлы как серебро, свинец и многие другие. К «легким» материалам относят магний с весом ниже чем у ванадия. Нельзя забывать и радиоактивных материалах, к примеру, вес урана составляет 19,05 грамм на кубический см. То есть, 1 кубический метр весит 19 тонн.
Удельный вес других материалов
Наш мир сложно представить без множества материалов, используемых в производстве и быту. Например, без железа и его соединений (стальных сплавов). УВ этих материалов колеблется в диапазоне одной – двух единиц и это не самые высокие результаты. Алюминий, к примеру, обладает низкой плотностью и малым удельным весом. Эти показатели позволили его использовать в авиационной и космической отраслях.
Удельный вес металлов
Медь и ее сплавы, обладают удельным весом сопоставимый со свинцом. А вот ее соединения – латунь, бронза легче других материалов, за счет того, в них использованы вещества с меньшим удельным весом.
Как рассчитать удельный вес металлов
Как определить УВ — этот вопрос часто встает у специалистов занятых в тяжелой промышленности. Эта процедура необходима для того, что бы определить именно те материалы, которые будет отличаться друг от друга улучшенными характеристиками.
Одна из ключевых особенностей металлических сплавов заключается в том, какой металл является основой сплава. То есть железо, магний или латунь, имеющие один объем будут иметь разную массу.
Плотность материала, которая рассчитывается на основании заданной формулы имеет прямое отношение к рассматриваемому вопросу. Как уже отмечено, УВ – это соотношение веса тела к его объему, надо помнить, что эта величина может быть определена как силу тяжести и объема определенного вещества.
Для металлов УВ и плотность определяют в той же пропорции. Допустимо использовать еще одну формулу, которая позволяет рассчитать УВ. Она выглядит следующим так УВ (плотность) равна отношению веса и массы с учетом g, постоянной величины. Можно сказать, что УВ металла может, носит название веса единицы объема. Дабы определить УВ необходимо массу сухого материала поделить на его объем. По факту, эта формула может быть использована для получения веса металла.
Кстати, понятие удельного веса широко применяют при создании металлических калькуляторов, применяемых для расчета параметров металлического проката разного типа и назначения.
УВ металлов измеряют в условиях квалифицированных лабораторий. В практическом виде этот термин редко применяют. Значительно чаще, применяют понятие легкие и тяжелые металлы, к легким относят металлы с малым удельным весом, соответственно к тяжелым относят металлы с большим удельным весом.
Источник
Плотность и удельный вес
Важнейшими характеристиками механических свойств жидкости являются ее плотность и удельный вес. Они определяют «весомость» жидкости.
Под плотностью ρ (кг/м 3 ) понимают массу жидкости т, заключенную в единице ее объема V, т.е.
Вместо плотности в формулах может быть использован также удельный вес γ (Н/м 3 ), т.е. вес G, приходящийся на единицу объема V:
Плотность и удельный вес жидкости связаны между собой. Эта связь легко устанавливается, если учесть, что G = mg:
1.3.2 Вязкость
Вязкость — это способность жидкости сопротивляться сдвигу, т. е. свойство, обратное текучести (более вязкие жидкости являются менее текучими). Вязкость проявляется в возникновении касательных напряжений (напряжений трения). Рассмотрим слоистое течение жидкости вдоль стенки (рисунок 1.3). В этом случае происходит торможение потока жидкости, обусловленное ее вязкостью. Причем скорость движения жидкости в слое тем ниже, чем ближе он расположен к стенке. Согласно гипотезе Ньютона касательное напряжение, возникающее в слое жидкости на расстоянии у от стенки, определяется зависимостью
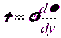
где dυ/dy — градиент скорости, характеризующий интенсивность нарастания скорости υ при удалении от стенки (по оси у).
Зависимость (1.5) называют законом трения Ньютона. Течения большинства жидкостей, используемых в гидравлических системах, подчиняются закону трения Ньютона, и их называют ньютоновскими жидкостями. Однако следует иметь в виду, что существуют жидкости, в которых закон (1.5) в той или иной степени нарушается. Такие жидкости называют неньютоновскими.
Величина μ, входящая в (1.5), получила название динамической вязкости жидкости. Она измеряется в Паּс либо в пуазах 1 Пз = 0.1 Па ּс. Однако на практике более широкое применение нашла кинематическая вязкость:
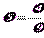
Е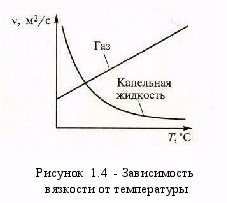
В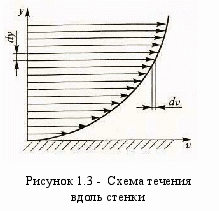
язкость жидкостей существенно зависит от температуры, причем вязкость капельных жидкостей с повышением температуры падает, а вязкость газов — растет (рисунок 1.4). Это объясняется тем, что в капельных жидкостях, где молекулы расположены близко друг к другу, вязкость обусловлена силами молекулярного сцепления. Эти силы с ростом температуры ослабевают, и вязкость падает. В газах молекулы располагаются значительно дальше друг от друга. Вязкость газа зависит от интенсивности хаотичного движения молекул. С ростом температуры эта интенсивность растет и вязкость газа увеличивается.
Вязкость жидкостей зависит также от давления, но это изменение незначительно, и в большинстве случаев его не учитывают.
1.3.3 Сжимаемость
Сжимаемость — это способность жидкости изменять свой объем под действием давления. Сжимаемость капельных жидкостей и газов существенно различается. Так, капельные жидкости при изменении давления изменяют свой объем крайне незначительно. Газы, наоборот, могут значительно сжиматься под действием давления и неограниченно расширяться при его отсутствии.
Для учета сжимаемости газов при различных условиях могут быть использованы уравнения состояния газа или зависимости для политропных процессов [4].
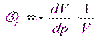
Знак минус в формуле обусловлен тем, что при увеличении давления объем жидкости уменьшается, т.е. положительное приращение давления вызывает отрицательное приращение объема.
При конечных приращениях давления и известном начальном объеме V можно определить конечный объем жидкости
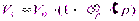
а также ее плотность
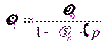
Величина, обратная коэффициенту объемного сжатия βр, называется объемным модулем упругости жидкости (или модулем упругости) К = 1/ βр (Па). Эта величина входит в обобщенный закон Гука, связывающий изменение давления с изменением объема
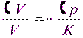
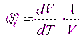
где dT— изменение температуры; dV— изменение объема под действием температуры; V — объем жидкости.
При конечных приращениях температуры
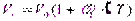
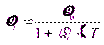
Как видно из формул (1.12), (1.13) с увеличением температуры объем жидкости возрастает, а плотность уменьшается.
Коэффициент температурного расширения жидкостей зависит от давления и температуры, так для воды при t = 0 0 C и p = 0,1 МПа βt = 14·10 –6 1/град, а при t = 100 0 C и p = 10 МПа βt = 700·10 –6 1/град, то есть изменяется в 50 раз. Однако на практике обычно принимают среднее значение в данном диапазоне температур и давления. Например, для минеральных масел
Газы весьма значительно изменяют свой объем при изменении температуры. Для учета этого изменения используют уравнения состояния газов или формулы политропных процессов [4].
1.3.5 Испаряемость
Любая капельная жидкость способна изменять свое агрегатное состояние, в частности превращаться в пар. Это свойство капельных жидкостей называют испаряемостью.

В 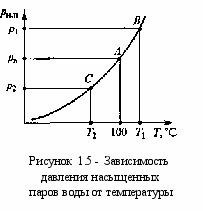
Такое давление называют давлением насыщенных паров рн.п... Величина рнп всегда приводится как абсолютное давление и зависит от температуры.
Для примера на рисунке 1.5 приведена зависимость давления насыщенных паров воды от температуры. На графике выделена точка ^ А, соответствующая температуре 100 °С и нормальному атмосферному давлению ра. Если на свободной поверхности воды создать более высокое давление р1, то она закипит при более высокой температуре Т1 (точка В на рисунке 1.5). И наоборот, при малом давлении р2 вода закипает при более низкой температуре Т2 (точка С на рисунке 1.5).
^ 1.3.6 Растворимость газов
Многие жидкости способны растворять в себе газы. Эта способность характеризуется количеством растворенного газа в единице объема жидкости, различается для разных жидкостей и изменяется с увеличением давления.
Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, то есть
При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказывается на работе гидросистем.
2 ГИДРОСТАТИКА
^ 2.1 Свойства гидростатического давления. Основное уравнение гидростатики
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение. В покоящейся жидкости возникают только напряжения сжатия и не могут действовать касательные напряжения, так как любое касательное напряжение жидкости вызовет ее движение, т.е. нарушит состояние покоя. В главе 1 было показано, что напряжения сжатия вызывает сила, действующая перпендикулярно на бесконечно малую площадку. Отсюда вытекает первое свойство гидростатического давления: гидростатическое давление действует по нормали к поверхности и является сжимающим, то есть действует внутрь рассматриваемого объема.
Второе свойство гидростатического давления состоит в том, что в любой точке внутри покоящейся жидкости гидростатическое давление не зависит от ориентировки площадки, по которой оно действует, то есть одинаково во всех направлениях.
Д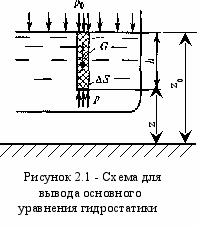
В выбранной точке искомое давление р действует по всем направлениям одинаково (второе свойство гидростатического давления). Но на выделенный объем создаваемая этим давлением сила действует по нормали к поверхности и направлена внутрь объема (первое свойство гидростатического давления), т.е. сила направлена вверх и равна произведению р на площадь ΔS. Тогда условием равновесия выделенного объема жидкости в вертикальном направлении будет равенство
Вес G выделенного цилиндра жидкости можно определить, подсчитав его объем V:
G = V∙ p ∙g = ΔS∙ h ∙ ρ ∙ g.
Подставив математическое выражение для G в уравнение равновесия и решив его относительно искомого давления р, окончательно получим
Величина р является одинаковой для всех точек объема жидкости, поэтому учитывая свойства гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля.
Давление жидкости, как видно из формулы (2.1), возрастает с увеличением глубины по линейному закону и на данной глубине есть величина постоянная. Поверхность, давление во всех точках которой одинаково, называется поверхностью уровня. В случае, когда на жидкость действует только сила тяжести, поверхности уровня представляют собой горизонтальные плоскости, при этом свободная поверхность является одной из поверхностей уровня.
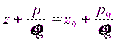
Так как рассматриваемая точка выбрана произвольно, можно утверждать, что для любой точки неподвижного объема жидкости
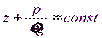
Основное уравнение гидростатики широко применяется для решения практических задач. Однако при его использовании в практических расчетах следует обращать особое внимание на высоту h, так как она может принимать как положительные, так и отрицательные значения.
При выборе знака в основном законе гидростатики всегда следует помнить, что чем ниже (глубже) располагается точка в данной жидкости, тем больше давление в этой точке.
В заключение следует добавить, что основное уравнение гидростатики широко используется при измерении давлений.
^ 2.2 Устройство и приборы для измерения давления
Как было показано в главе 1, давление может быть абсолютным, избыточным и давлением вакуума. В машиностроительной гидравлике наиболее часто используются давления избыточные и вакуума, поэтому измерению этих давлений уделим наибольшее внимание.
Простейшим прибором для измерения избыточного давления является пьезометр, который представляет собой вертикально установленную прозрачную трубку, верхний конец которой открыт в атмосферу, а нижний присоединен к емкости, в которой измеряется давление (рисунок 2.2, а). Применяя формулу (2.1) к жидкости, заключенной в пьезометре, получим
где рабс — абсолютное давление в жидкости на уровне присоединения пьезометра,
Отсюда высота подъема жидкости в пьезометре (пьезометрическая высота)
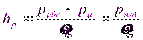
Таким образом, пьезометрическая высота представляет собой высоту столба жидкости, соответствующую избыточному давлению в данной точке.
С помощью стеклянной трубки можно измерить и давление вакуума, при этом жидкость в трубке опустится ниже уровня измерения (см. рисунок 2.2,б). В этом случае
откуда 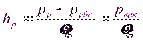
Формула (2.4) позволяет определить максимальную высоту всасывания жидкости. Полагая рабс = 0 и не учитывая давления насыщенных паров, получаем
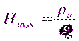
При нормальном атмосферном давлении (0,1033 МПа) высота Нmax для воды равна 10.33 м, для бензина – 13,8 м, для ртути – 0,760 м и так далее.
С
хемы наиболее распространенных жидкостных манометров и вакуумметров представлены на рисунке 2.3.
Рисунок 2.3 – Схемы жидкостных манометров:
а) U – образный манометр; б) чашечный манометр; в) дифференциальный манометр;
г) двух-жидкостный микроманометр; д) двух-жидкостный чашечный манометр.
П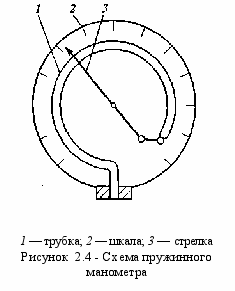
Аналогичные по принципу работы приборы с использованием ртути позволяют в 13,6 раза уменьшить пьезометрические высоты (ртуть в 13,6 раза тяжелее воды). Но ртуть ядовита, и такие приборы в машиностроении практически перестали применяться.
Широкое распространение в технике для измерения давлений получили пружинные манометры. Основным элементом такого прибора (рисунок 2.4) является пружинящая тонкостенная трубка 1 (обычно латунная). Один из концов трубки запаян и подвижен, а второй закреплен, и к нему подводится измеряемое давление. Подвижный конец трубки 1 кинематически связан со стрелкой 3. При изменении давления он изменяет свое положение и перемещает стрелку 3, которая указывает на соответствующее число на шкале 2.
Пружинные приборы для измерения вакуума не имеют ни принципиальных, ни конструктивных отличий от пружинных манометров. Устройства для измерения вакуума получили название вакуумметров.
Выпускаются также приборы, позволяющие измерять как избыточные давления, так и вакуум. Их принято называть мановакуумметрами.
В метеорологии измерение абсолютных значений атмосферных давлений проводят с помощью барометров. Для машиностроительных систем измерение абсолютных давлений практического значения не имеет.
^ 2.3 Сила давления на плоскую стенку
Д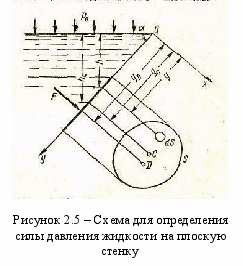
При определении силы, действующей со стороны жидкости на плоскую стенку, рассмотрим общий случай, когда стенка наклонена к горизонту под углом α, а на свободную поверхность жидкости действует давление р (рисунок 2.5).
Вычислим силу давления F, действующую на некоторый участок рассматриваемой стенки площадью S. Ось Ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось Оу — перпендикулярно к этой линии в плоскости стенки.
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS:
dF = p dS = (pо + ρ gh) dS = pо dS + ρ g h d S,
где ро — давление на свободной поверхности;
h — глубина расположения площадки dS.
Для определения полной силы F проинтегрируем полученное выражение по всей площади S:
где у — координата площадки dS.
Последний интеграл представляет собой статический момент площади S относительно оси Ох и равсн произведению этой площади на координату ее центра тяжести (точка С), то есть
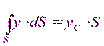
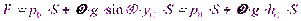
здесь hс — глубина расположения центра тяжести площади S.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник